R1(2019年)理論　問5　 第三種電気主任技術者試験（電験三種）丁寧に解いていく（過去問解法）（国家資格）

今回は令和1年（2019年）理論の問5を解いていきます。

これは簡単な問題ですね。

一個づつ電圧を求めていきましょう

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋

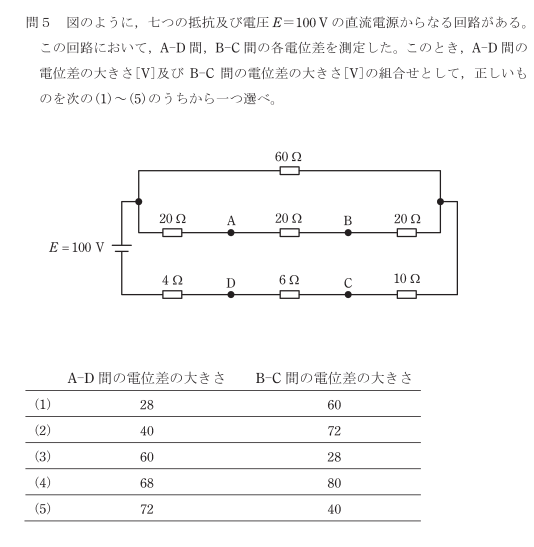
わかりやすく、並べ替えます

合成抵抗を求めます

直列抵抗は足し算です

並列抵抗は
\(\displaystyle R_0=\frac{R_1R_2}{R_1+R_2}\)

並列の抵抗が等しい場合は
\(\displaystyle R_0=\frac{R_1R_1}{R_1+R_1}=\frac{R_1}{2}\)

抵抗値は半分になります

次に、分圧を使って\(R_{1234}とR_{567}\)にかかっている電圧を計算します
\(\displaystyle V_{1234}=\frac{30Ω}{30Ω+20Ω}100V=60V\)

\(\displaystyle V_{567}=\frac{20Ω}{30Ω+20Ω}100V=40V\)

かかっている電圧がわかったので
次は\(R_2、R_3、R_4\)にかかっている電圧を求めます

両端に60Vかかっているので分圧を使います

\(\displaystyle V_2=\frac{20Ω}{20Ω+20Ω+20Ω}60V=20V\)

抵抗が等しいので\(V_2=V_3=V_4=20V\)です

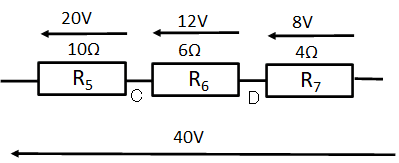
次は\(R_5、R_6、R_7\)にかかっている電圧を求めます

両端に40Vかかっているので分圧を使います

\(\displaystyle V_5=\frac{10Ω}{20Ω}40V=20V\)

\(\displaystyle V_6=\frac{6Ω}{20Ω}40V=12V\)

\(\displaystyle V_7=\frac{4Ω}{20Ω}40V=8V\)

となります

電圧の計算ができたので電位を計算していきます
A点：100V-20V=80V
B点：100V-20V-20V=60V
C点：100V-20V-20V-20V-20V=20V
D点：100V-20V-20V-20V-20V-12V=8V
となります

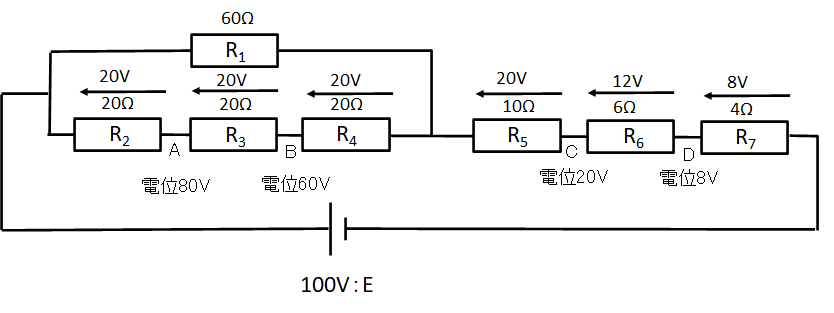
だから\(V_{AD}、V_{BC}\)は
\(V_{AD}=V_A-V_D=80V-8V=72V\)
\(V_{BC}=V_B-V_C=60V-20V=40V\)
です

正解は(5)です

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋